
This value of σ is different than that estimated by the average range, which was 8.36. For the data in Table 1, the average standard deviation and σ are given by: The values of c 4 are shown in Table 2 above. Where c 4 is constant that depends on subgroup size. The standard deviation is then estimated from the following equation: Where s i is the standard deviation of the i th subgroup and k is the number of subgroups. When the subgroup size is constant, the average of the subgroup standard deviations is given by: The average of the subgroup standard deviations could also be used to estimate the standard deviation. The X control chart for these data is shown in Figure 1.įigure 1: X Based on Sigma from Average Range So, both methods for calculating the control limits are equivalent. For a table of these values, please see our newsletter our X-R control charts. This is the value of A 2 for a subgroup size of 3 that you find in the tabulated control chart constants for A 2. Substituting in d 2 and n for our example gives: Substituting for R and solving for A 2 gives: There are two different equations for the UCL above, which must give the same result. Where A 2 is a constant that depends on subgroup size. You probably use the following equations: You may not be used to calculating control limits this way for the X chart. Using the estimate of the standard deviation from the average range, we can now calculate the control limits: From the table, you can see that d 2 for a subgroup size of 3 is 1.693.įor the data in Table 1, the average range and σ are given by: Table 2 shows the values of d 2 based on subgroup sizes up to 20. Where d 2 is a constant that depends on subgroup size. Where R i is the range of the i th subgroup and k is the number of subgroups. The average range is simply the average of the subgroup averages when the subgroup size is constant: The average of the subgroup ranges is the classical way to estimate the standard deviation. Average of the subgroup standard deviations.We will look at three methods for estimating σ for subgroup data: The value of σ depends on the method you use to estimate it. These control limit equations may be different from the ones you normally use. Remember: the standard deviation of the subgroup averages is equal to the standard deviation of the individual values divided by square root of the subgroup size. Where UCL and LCL are the upper and lower control limits, n is the subgroup size, and σ is the estimated standard deviation of the individual values. Control limits for the X chart are given by: These impact how control limits are calculated. We will look at three different ways to estimate the standard deviation. Three Ways to Estimate the Standard Deviation

There may be some minor differences due to rounding.
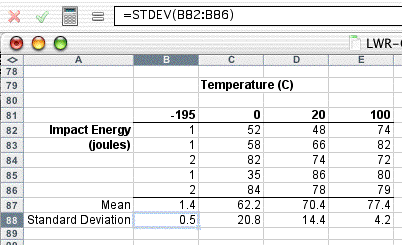
The overall sum and average are given for subgroup averages, subgroup ranges and subgroup standard deviations – again for use below. The subgroup average, range and standard deviation have also been calculated for use below.

So, our subgroup size is constant for each of the 10 subgroups. We have 10 subgroups, each containing 3 observations or results. The data we will use are shown in the table.
#How to get standard deviation in excel graph software
Sometimes people ask why some software packages give different values for the control limits. The standard deviation is a little more difficult to understand – and to complicate things, there are multiple ways that it can be determined – each giving a different answer. The average is easy to calculate and understand – it is just the average of all the results. One of the purposes of control charts is to estimate the average and standard deviation of a process.


 0 kommentar(er)
0 kommentar(er)
